The Battle of Chibi

作者 macorhard

题目翻译

题面

给定一个长度为N的数列A，求A有多少个长度为M的严格递增子序列。

数据范围

1<=M<=1000,序列A中的数的绝对值不超过10^9.因为答案可能很大，你只需要输出对1e9取模后的结果。

设F[i][j]表示A的前j个数构成的以Aj为结尾的数列中，长度为i的严格递增子序列有多少个.

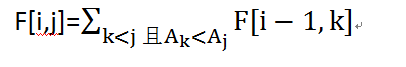
在上式中，i和j都可以看作“阶段”，只会从小往大转移。k是DP的“决策”，有两个限制条件k<j和Ak<Aj。我们先写出枚举k的朴素程序

const int mod=1e9;
memset(f,0,sizeof(0));
a[0]=-(1<<30);//INF
a[0][0]=1;
for(int i=1; i<=m; i++)
	for(int j=1; j<=n; j++)
		for(int k=0; k<j; k++)
			if(a[k]<a[j])
				f[i][j]=(f[i][j]+f[i-1][k])%mod;
int ans=0;
for(int i=1; i<=n; i++)
	ans=(ans+=f[m][i])%mod;

在内层循环j和k进行时，可以把外层循环变量i看作定值。我们可以发现，当j增加1时，k的取值范围从0<=k<j变为 0<=k<j+1，也只是多了k=j这1新决策。所以我们需要维护一个支持如下操作的决策候选集合，其中每个决策可以用一个二元组（Ak，F[i-1,k]）来存储：

  1. 插入一个新的决策。具体来说，在j增加1前把 （Ak，F[i-1,k]） 加入集合。
  2. 给定一个值 Aj ，查询满足 Ak<Aj 的二元组对应的 F[i-1,k] 的值。

若把二元组Ak看作关键码， F[i-1,k] 看作权值，这就是一个经典的支持插入，查询前缀和的数据结构问题，用平衡树可以直接解决。

当然，因为平衡树难度实现很大，我们可以把数列A中的所以数值离散化到[2,N+1]之间，设val（x）表示x离散化之后的数值。特殊的，我们令A0=- ∞ ，val(A0)=1然后在[1,N+1]之间建立树状数组，起初所有值为0

  1. 对于插入决策的操作，就把val(Ak)位置上的值增加F[i-1][k]。
  2. 对于查询操作，就在树状数组中计算[1,val(Aj)-1]的前缀和
for(int i=1;i<=m;i++)
{
	memset(c,0,sizeof(c))//c为储存树状数组的数组
	add(val(a[0],f[i-1][0])); 
	for(int j=1;j<=n;j++)
	{
		f[i][j]=ask(val(a[j])-1);
		add(val(a[j]),f[i-1][j]);
	}
}

综上所述，我们简单使用树状数组来维护前缀和，就把动态规划的时间复杂度优化到了O(NM log N)

留下评论